
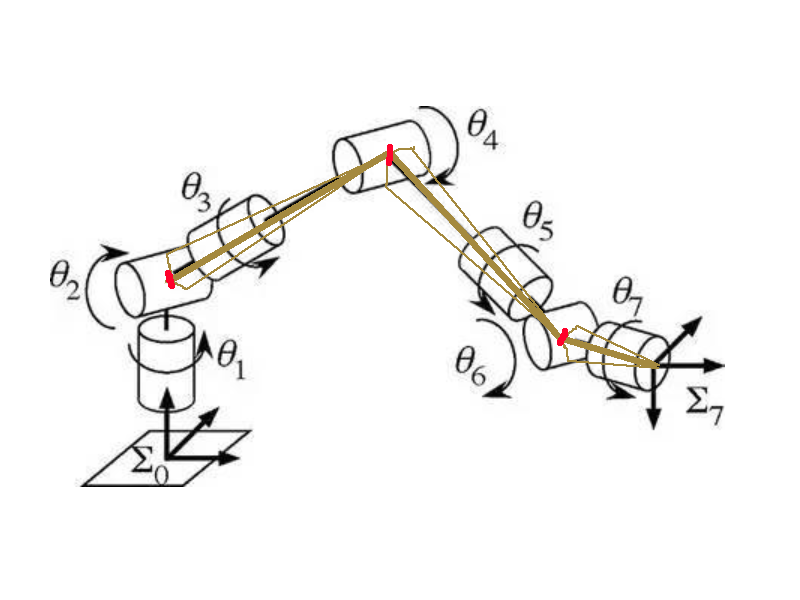
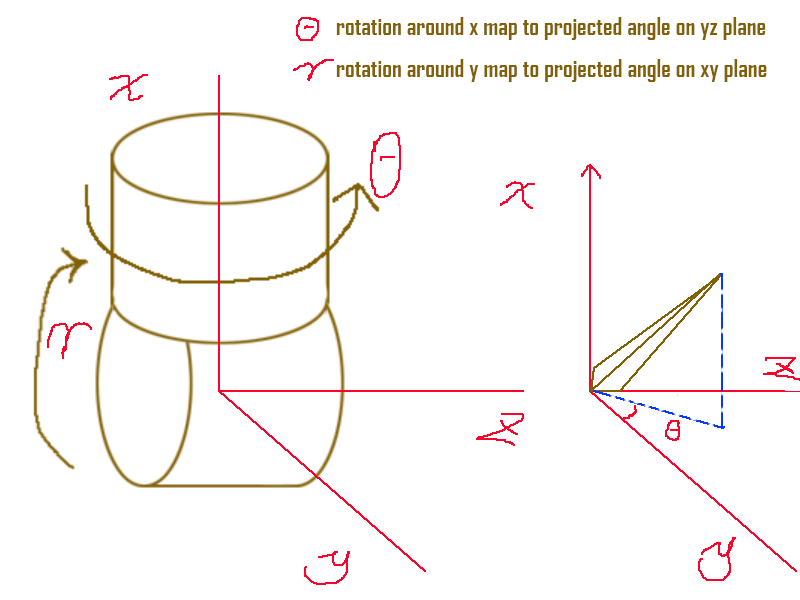
一种简单的7自由度机器臂的抽象图。
robot arm abstraction.
把它分解每2个圆柱一个单元的形式。
Split this kind of arm into elementary part.
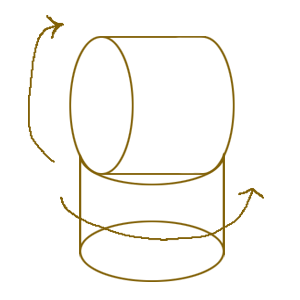
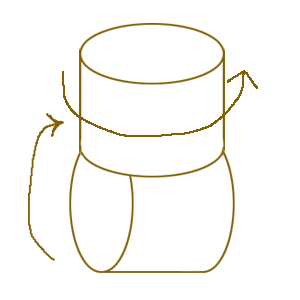
把每个单元对应于一根骨骼(如3dmax里的骨骼)
think this kind of element into a bone.
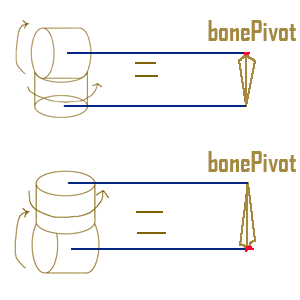
然后7自由度器械臂就可以转化为下图
Then the robot arm can be
然后,就可以用通常用的动画系统里的IK去解算这个骨骼,如实时引擎unity里的finalIK系统。其中CCD算法比较简单值观还有旋转约束。
solve those connected bone with generic animation IK method(Like CCD of finalIK in unity engine, and they can be solved with angle limits).
动画IK计算好骨骼运动信息后,就要把骨骼旋转映射回机械臂。
Map back bone rotation into element rotation.
有时间 就做个Unity的demo,别说我懒。
I will try to made a Unity demo sooner or later :P
更广泛的机械臂模拟 使用的是线性代数矩阵的解法。 建立DH坐标系确定动力学参数。虽然我在研究但实在是麻烦不直观。但是适用性应该更广。
简单推算的IK解算,还未编码验证。这部分如果用unity引擎模拟则可用finalIK等插件不必自己手动编码。
simple IK solver draft idea.
2端骨骼的解算
solve 2 bones
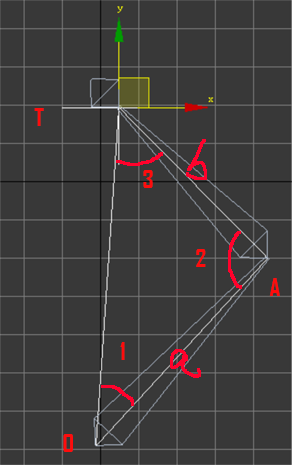
骨骼起始点是O
bone start position:O
解算目标点是T
target:T
骨骼是a,b和b末端的一个辅助骨骼
bone a, bone b and a dummy bone link
骨骼a,b和OT的长度已知,则角度1,2,3都可求。
length of a,b,OT is known so all the angle(1,2,3) in this triangle can be solved.
A的位置则是在一个3维空间的圆形上,这个圆形可以保持角度1,2,3是不变的。这个圆就是A点的所有解。
position of A is on a circle which when A is on the circle angle(1,2,3) will not change.
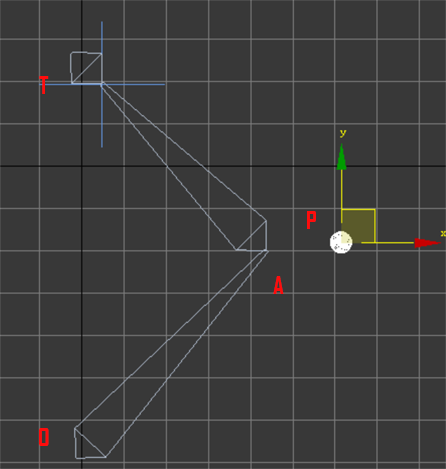
另外引入一个参照物P,在平面TPO上就可以确定唯一点P。
with a refer position P. A can be solved on plan TPO.
3端骨骼的解算
solve 3 bones
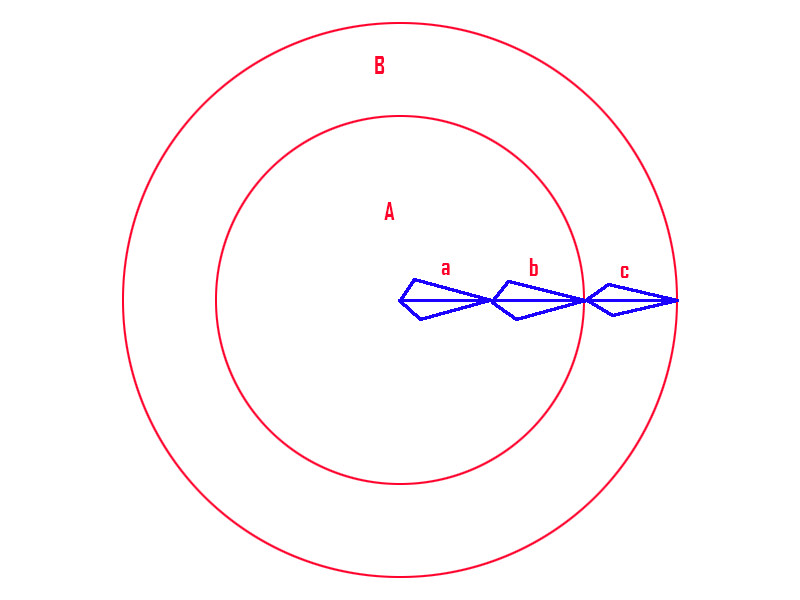
如图示骨骼a,b,c 圆A半径是骨骼a和b长度和 圆B半径是骨骼a,b,c长度和。A,B可以作为球形方便画图都做平面圆,目标点是T。
bone a,b,c
area A with radius = length(a) + length(b)
area B with radius = length(a) + length(b) + length(c)
A,B can be 3d sphere but for simple here use 2D area
target:T
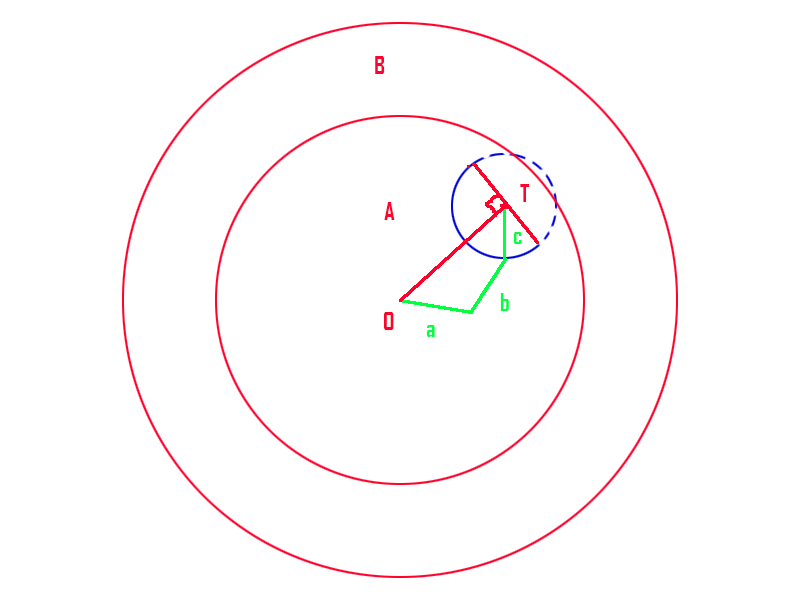
T在A内的时候,骨骼起始位置为O,以T为圆心骨骼c的长为半径做圆,连接OT,找到和OT垂直的半径,在OT这边的半圆(图中蓝色实线部分)取一点作为骨骼c的位置,再用之前提过的解决2端骨骼的方法接触另外2端。
T inside A
start point:O
target point:T
solve IK for T
draw a circle with radius = length(c)
find a diameter which perpendicular to OT
half of circle on the OT side can be solved as position of bone c.
solve bone a,b use the "solve 2 bones" method mentioned above.
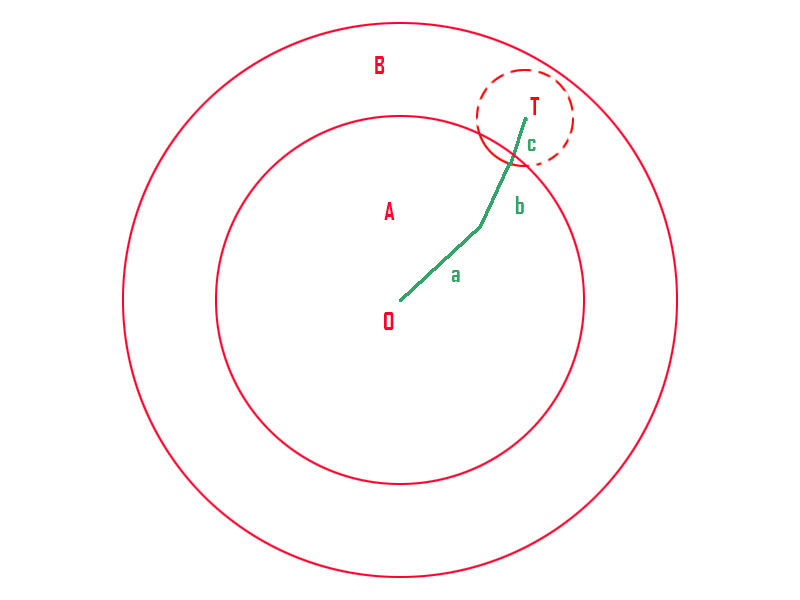
T在A外B内的时候,骨骼起始位置为O,以T为圆心骨骼c的长为半径做圆,找到与圆形A相交的部分(图中红色实线部分)取一点作为骨骼c的位置,再用之前提过的解决2端骨骼的方法接触另外2端。
T outside A inside B
draw a circle with radius = length(c)
find intersection part with area A.
point on the intersection part can be solved as position of bone c .
solve bone a,b use the "solve 2 bones" method mentioned above.